I wanted to review DataDog again, and take a look at how the current chart is shaping out. I took a look at this stock about a month ago, you can see the article here. In that blog I was explaining the scenario for a minor pullback, then further upside. Lets take a look at the chart I was presenting.
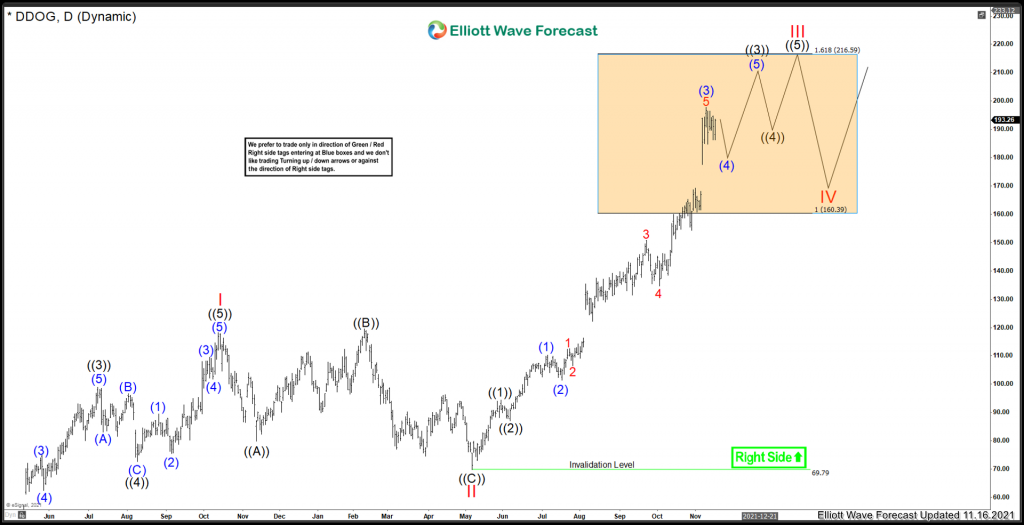
Datadog Elliottwave November 17/2021 view:
At the time, the evidence supported the idea that this stock was in a wave III advance. I was looking for the 1.618 extension as a possible target area for where Red III could possibly peak. Lets fast forward a month later and see how things turned out.
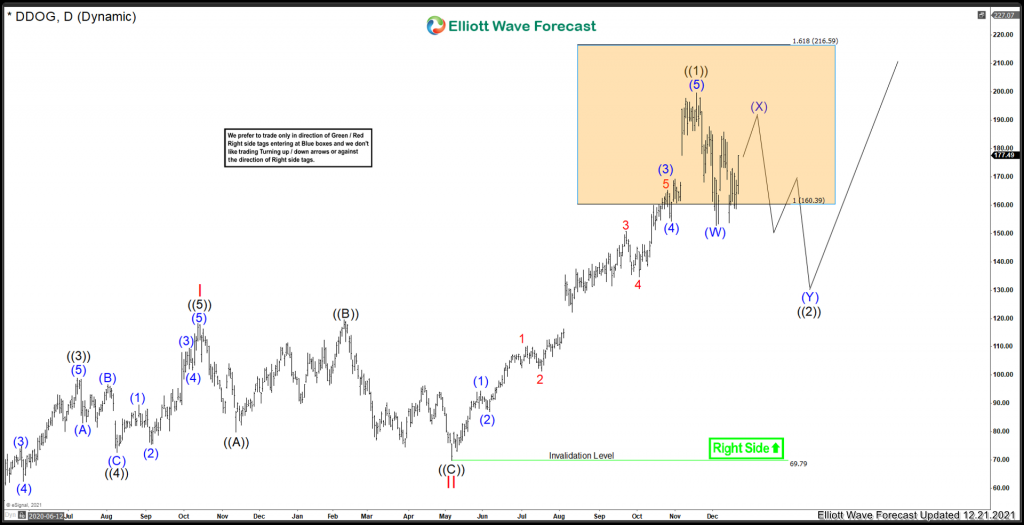
DataDog Elliotwave December 21/2021 view:
One thing is clear right now, this stock is correcting the cycle from May 2021 low right now. The only question at this time is; Is this a wave IV correction against that low, or a nest?
I would like to suggest that a nest in ((2)) is taking place. This is actually very similar to my original analysis that I blogged about back in July 2021 (you can see the blog here). In July, I was looking for a rally from the May 2021, to create a Nest before advancing higher. With current price action, the wave didn’t extend high enough for a Red III, and failed to reach the 1.618 extension where a Red III could peak. The momentum is suggesting that a correction against that May 2021 low is taking place. So instead of a wave III peak, I favour nesting before a wave 3 of 3 advance takes place in the months to come.
Where can DataDog head from here in the shorter cycles? The area for Blue (X) can peak is the 187 area equal leg. Never sell (short) a 3 waves decline down. Right now, DataDog has complete 3 waves back from the ((1)) peak. A double correction is favoured as the Indices and Technology $NQ_F have not reached ideal areas to strike a low, so for now, further downside is favoured.
Once (X) is set, we can get an idea area for where ((2)) can stike a low. Without an equal leg to measure, I can point to the 50% to 61.8% retrace of the Red II to ((1)) leg. This comes at 134.82 to 119.48. This would be the ideal area for ((2)) to bottom.